Quote:
Originally Posted by mudra
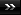

Chesterton Windmill nr Harbury Warwickshire. Reported 9th July.
This crop Circle represents a tetrahedron in a circle. In geometry is a platonic solid.
From Wiki : “The Platonic solids feature prominently in the philosophy of Plato for whom they are named. Plato wrote about them in the dialogue Timaeus c.360 B.C. in which he associated each of the four classical elements (earth, air, water, and fire) with a regular solid. Earth was associated with the cube, air with the octahedron, water with the icosahedron, and fire with the tetrahedron. There was intuitive justification for these associations: the heat of fire feels sharp and stabbing (like little tetrahedra). Air is made of the octahedron; its minuscule components are so smooth that one can barely feel it. Water, the icosahedron, flows out of one's hand when picked up, as if it is made of tiny little balls. By contrast, a highly un-spherical solid, the hexahedron (cube) represents earth. These clumsy little solids cause dirt to crumble and break when picked up, in stark difference to the smooth flow of water. The fifth Platonic solid, the dodecahedron, Plato obscurely remarks, "...the god used for arranging the constellations on the whole heaven". Aristotle added a fifth element, aithêr (aether in Latin, "ether" in English) and postulated that the heavens were made of this element, but he had no interest in matching it with Plato's fifth solid…
In the 16th century, the German astronomer Johannes Kepler attempted to find a relation between the five known planets at that time (excluding the Earth) and the five Platonic solids. In Mysterium Cosmographicum, published in 1596, Kepler laid out a model of the solar system in which the five solids were set inside one another and separated by a series of inscribed and circumscribed spheres. The six spheres each corresponded to one of the planets (Mercury, Venus, Earth, Mars, Jupiter, and Saturn). The solids were ordered with the innermost being the octahedron, followed by the icosahedron, dodecahedron, tetrahedron, and finally the cube. In this way the structure of the solar system and the distance relationships between the planets was dictated by the Platonic solids. In the end, Kepler's original idea had to be abandoned, but out of his research came the discovery of the Kepler solids, the realization that the orbits of planets are not circles, and Kepler's laws of planetary motion for which he is now famous.”
http://www.cropcircleconnector.com/2.../comments.html
Love always
mudra |
From the Cassiopaean Transcripts
session 19/12/1998
Q: (A) You get what we may call a time form and this time form is sometimes like any other physical field. So, of course the different possibilities that I can
mathematically model: time form, time vacuum, different times, time loops, and other things. These are interesting possibilities that I have, provided I use
something similar to Kaluza-Klein. Did I miss something?
A: It is not that you miss something; it is merely that you have not yet found the something.
Q: (A) What is this something?
A: Tetrahedron.
Q: (A) Okay, at some point we were talking about a 3 dimensional matrix, 12x12x12. I was wondering where this 12 comes from, and I was thinking that 12 is
2x6 and I was supposed to be looking at hexagons, and a hexagon represents 6 dimensions, four pluses and two minuses. If I add to this 6 energies
corresponding to 6 dimensions, then I have 12 dimensions, and this would account for number 12. Is this correct?
A: Yes.
Q: (A) Now, this all has something to do with gravity, and at some point you said that all this gravity/anti-gravity business is just the way, and that the main goal
is to attain higher knowledge. What is this higher knowledge; what kind of higher knowledge?
A: You are on the path.
session 25/09/1999
Q: There could be many explanations. Now, we have a correspondent who wrote and asked a question. He said that he noticed there was promotion of
Hoagland's idea about the 19.5 degree tetrahedral configuration at one point, and then another idea regarding the parallelogram business involving an 18 degree
mark in another section. So, what is the difference between the 19.5 degree comments of Hoagland, and the 18 degree point of interest that you brought up?
Are we talking about two different things here?
A: Well, if you do the math, you see that 18 degrees fits nicely with ninety. Maybe 19.5 is due to crustal slippages in some" land mark" event?!
Q: (A) But, in geometry, this 19.5 degrees is what you get when you try to put a tetrahedron into a sphere. That's how Hoagland got it, not because of
observation.
A: Okay, that is good, too.
Q: How come you didn't know that?
A: We pointed it out in the first place.
Q: Is that why you put "landmark" in quotes? That 19.5 is where it touches. It is the mark of the point of contact. Is that it?
A: Clues, my dear, clues, and the eternal need not to abridge free will.
Q: But, if these tetrahedrons fit in a sphere, and they touch the sphere at 19.5 degrees, how do they relate to this effect that you have said manifests at 18
degrees?
A: Does 1.5 fit into 90? Does 90 fit into 180? Does 180 fit into 360? Ask yourself, "What does it mean?"
Q: We don't know. (A) The point is that the angle Hoagland is talking about is not 19.5, it is an approximation of point something, something, something.... So,
if it is just 19.5, that's the difference between 19.5 and 18 - that is 1.5, which, in this case, is not exactly 1.5, it's one point something which does not fit into
anything that we know.
A: Circumference.
Q: (A) Yes. 360 degrees. Is the circumference important?
A: It is important.
Q: (A) So, we can compute these two circumferences, and these will differ by some number, and this number will fit again into one of these circumferences, and
the point is that it should fit so that there is an integer number...
A: Yes.
Q: (A) But, there will then be many more angles. There will be not only 18 and 19.5...
A: Yes. All Hoagland has done is highlight a point at which magnetic lines converge using the tetrahedron model.
Q: If they converge at that point...
A: But the question is how does the tetrahedron model relate to trans-dimensional space?
Q: How does the tetrahedron model relate to trans- dimensional space?
A: A key which unlocks the door.
Q: Speaking of a key that unlocks a door: there is some information going around that a gigantic computer has been installed inside the earth that was put there
by a Reptilian race, and that the recovery of this thing is one of the reasons for the current or upcoming "invasion" by them. Does this tetrahedron configuration
in the earth relate to some giant alien computer?
A: No.
Q: Is there a giant alien computer buried in the Earth?
A: Not likely that.
Q: Back to the tetrahedron. How is it a key to trans- dimensional space? Does one activate it in some way? Do you place machinery of some sort at these
points?
A: No. Magnetism.
Q: Are you supposed to generate magnetism, or is it natural magnetism?
A: Natural.
Q: Are you supposed to do anything to it or with it?
A: Supposed???
Q: Is it useful to do something with it?
A: Can be.
Q: In what sense?
A: Traveling between dimensions.
Q: Is anybody at the present time utilizing it in this way?
A: Not terran STS 3rd density.
Q: That implies that 4th density STS IS doing this. Could one construct a scale model of a tetrahedron in a sphere, magnetize it, and open portals?
A: Yes.
Q: Would it require a lot of electrical current?
A: Yes.
Q: Is there anyway to travel between dimensions, in space time, or whatever, utilizing very little power, as such?
A: Off the point we told you before that all spheres of cosmic nature are windows.